Exponential decay
From Wikipedia, the free encyclopedia
A quantity is said to be subject to exponential decay if it decreases at a rate proportional to its value. Symbolically, this can be expressed as the following differential equation, where N is the quantity and λ is a positive number called the decay constant.
The solution to this equation (see below for derivation) is:
Here N(t) is the quantity at time t, and N0 = N(0) is the initial quantity, i.e. the quantity at time t = 0.

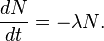
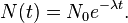

No comments:
Post a Comment