Half-life
A more intuitive characteristic of exponential decay for many people is the time required for the decaying quantity to fall to one half of its initial value. This time is called the half-life, and often denoted by the symbol t1 / 2. The half-life can be written in terms of the decay constant, or the mean lifetime, as:
When this expression is inserted for τ in the exponential equation above, and ln2 is absorbed into the base, this equation becomes:
Thus, the amount of material left is 2 − 1 = 1 / 2 raised to the (whole or fractional) number of half-lives that have passed. Thus, after 3 half-lives there will be 1 / 23 = 1 / 8 of the original material left.
Therefore, the mean lifetime τ is equal to the half-life divided by the natural log of 2, or:
 .
.
E.g. Polonium-210 has a half-life of 138 days, and a mean lifetime of 200 days.
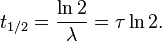
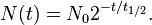

No comments:
Post a Comment