Solution of the differential equation
The equation that describes exponential decay is
or, by rearranging,
Integrating, we have
where C is the constant of integration, and hence
where the final substitution, N0 = eC, is obtained by evaluating the equation at t = 0, as N0 is defined as being the quantity at t = 0.
This is the form of the equation that is most commonly used to describe exponential decay. Any one of decay constant, mean lifetime or half-life is sufficient to characterise the decay. The notation λ for the decay constant is a remnant of the usual notation for an eigenvalue. In this case, λ is the eigenvalue of the opposite of the differentiation operator with N(t) as the corresponding eigenfunction. The units of the decay constant are s-1.


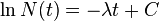
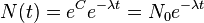

No comments:
Post a Comment